学校生活の様子
卒業証書授与式に向けて
お礼の手紙(6年生)
あっぱれ!
できたよ!
過日アップした正方形の面積をもとめる問題について、子供たちが、「うちのお父さん、できたよ!」「お母さんが、簡単だった。って言っていました。」などと、反応がありました。子供たちは、次のように説明してくれました。
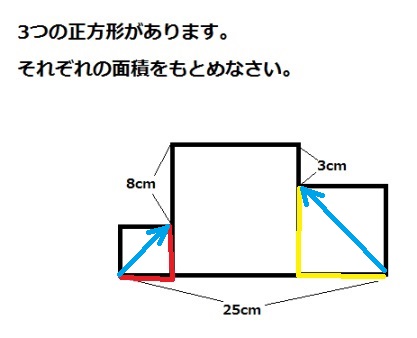
まず、25cmのところにある、赤い線と黄色い線を真ん中の正方形に移動します。その後、8cmと3cmの部分を合わせると、紫の線のように見ることができます。紫の線は、大きな正方形の3辺と等しくなります。3等分すると、大きな正方形の一辺の長さになりますね。大きな正方形の12cmです。
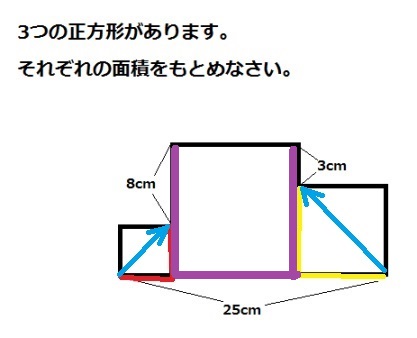
12ー8=4 これが小さな正方形の1辺の長さ。12-3=9 これが中ぐらいの正方形の1辺の長さ。
12×12+4×4+9×9 この式で、3つの正方形の面積が求められます。xやy等を使わなくても、このように求めることができますね。5,6年生より4年生の方ができがよかったのも、納得がいく気がしませんか?
おや?
4,5,6年生に次のような問題を出してみました。
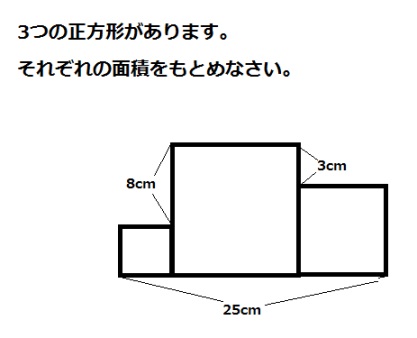

すると、6年生より5年生、5年生より4年生のほうが、正解にたどり着くのほうが早かったんです。
不思議な感じがしますね。4年生より6年生のほうが、圧倒的に知識が豊富で、難問をクリアできるのが普通です。
でも、この問題は、4年生のほうができがよかったんです。
なぜこのようなことが起こるか、認知心理学の学習論で説明されています。
新しいことを学ぶ際、以前できたことが突然わからなくなることがあります。
これを、「学習によるエラー」というそうです。
おそらく、保護者の皆さんは、xやyを使って連立方程式を使ったり、一辺の長さをxに置き換えて答えるのではないでしょうか?
実は、文字を使わなくても求めることができます。
子供たちは、日々、新しいことを学んでいます。
新しいことを学ぶ時、下学年でできたことができなくなるのは、より高いレベルに到達する上で、通過するプロセスの一つになるようです。
いかがですか?
頭の中がごちゃごちゃするのは、頭がいいことの証と言えそうですね。
こんなことを心の中において、子供たちの「学び」を見守っていきたいです。
不思議な感じがしますね。4年生より6年生のほうが、圧倒的に知識が豊富で、難問をクリアできるのが普通です。
でも、この問題は、4年生のほうができがよかったんです。
なぜこのようなことが起こるか、認知心理学の学習論で説明されています。
新しいことを学ぶ際、以前できたことが突然わからなくなることがあります。
これを、「学習によるエラー」というそうです。
おそらく、保護者の皆さんは、xやyを使って連立方程式を使ったり、一辺の長さをxに置き換えて答えるのではないでしょうか?
実は、文字を使わなくても求めることができます。
子供たちは、日々、新しいことを学んでいます。
新しいことを学ぶ時、下学年でできたことができなくなるのは、より高いレベルに到達する上で、通過するプロセスの一つになるようです。
いかがですか?
頭の中がごちゃごちゃするのは、頭がいいことの証と言えそうですね。
こんなことを心の中において、子供たちの「学び」を見守っていきたいです。








.JPG)















.JPG)
.JPG)
.JPG)
.JPG)




.JPG)
.JPG)


.JPG)
